
LeetCode - 28 Days Leeter Part 1
- Authors

- Name
- Stephen ♔ Ó Conchubhair
- Bluesky
- @stethewhitefox.bsky.social
Introduction
For 28 days "Leeter" part one and two, I have selected 14 coding patterns, 7 in each post. This is my approach to solving LeetCode problems. Here are the first 7 patterns with LeetCode problem solutions and how they can be effectively used to learn and solve LeetCode problems:
- 1. Prefix Sum
- 2. Two Pointers
- 3. Sliding Window
- 4. Fast & Slow Pointers
- 5. In-place Reversal of a Linked List
- 6. Breadth-First Search (BFS)
- Start Over with NeetCode 150
- 7. Overlapping Intervals
1. Prefix Sum
The Prefix Sum Pattern involves preprocessing an array to calculate cumulative sums, allowing for efficient range queries. The goal is to find a pivot index where the sum of all elements to the left of the pivot is equal to the sum of all elements to the right of the pivot.
Let's understand the pattern using the LeetCode problem 724. Find Pivot Index Find Pivot Index. The task is to find the index pivot or point where the sum of elements to the left of the index equals the sum of elements to the right of the index.
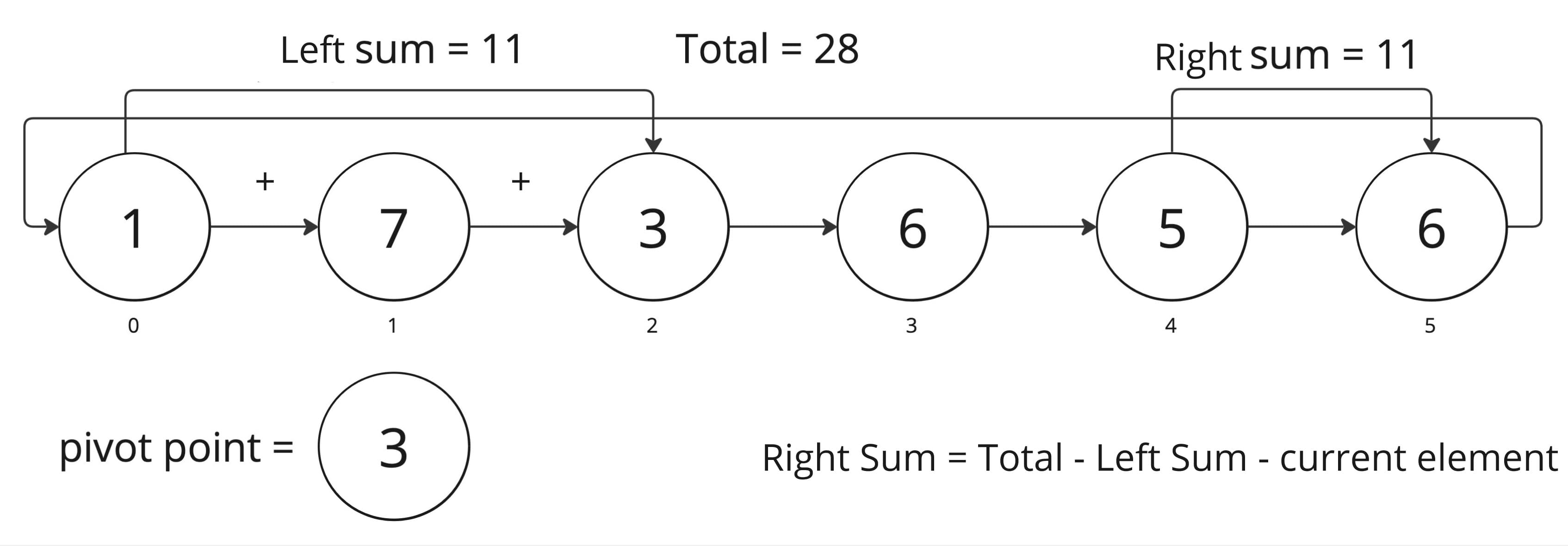
Pseudocode solution for Find Pivot Index (Brute Force 💪)
function findPivotIndex(nums):
// iterate through the array
for i from 0 to length of nums - 1:
leftSum = 0
rightSum = 0
// calculate the sum of the elements to the left of index i
for j from 0 to i - 1:
leftSum += nums[j]
// iterate through the array adding 1 to i until rightSum is equal to left
for k from i + 1 to length of nums - 1:
rightSum += nums[k]
leftSum === rightSum: return i
return -1 // Return -1 no pivot index is found
const nums: number[] = [1, 7, 3, 6, 5, 6]
console.log(findPivotIndex(nums)) // OUTPUT index: 3
Prefix Sum Pattern in TS Solution
Intuition
Using the prefix sum pattern. Create and Initialize three vars totalSum, leftSum and rightSum of type number. Use reduce method to calculate totalSum of the elements in the array then for loop thru array to find the pivot index while calculating the rightSum condition to check right sum is equal to the left sum, then the current index is the pivot and return index not found.
Step-by-Step Approach:
- Initialize:
totalSumUsing "reducer": Array.prototype.reduce() method, calculate the total sum of elements in the array.leftSumto store the sum of all the numbers strictly to the left of the index.rightSumto store the sum of all the number to the right of the index.
- Loop Through Array:
- Use a for loop to iterate through each index
i - For each index
i, calculaterightSumby subtractingleftSumandnums[i]fromtotalSum - If
leftSumequalsrightSum, returnias the pivot index. - If not, add
nums[i]toleftSum(soleftSumwill be ready for the next iteration).
- No Pivot: If the loop completes without finding a pivot, return
-1.
Complexity
Time complexity: 𝑂(𝑛) No nested loops (as in brute force solution) in the order of 𝑛, 𝑛 being the number of elements in the array a single pass by leveraging the prefix sum.
Space complexity: 𝑂(1) constant space using a fixed amount of memory.
const pivotIndex = (nums: number[]): number => {
// Calculate the total sum of the array in one pass
// removes the need for a first loop in the brute
const totalSum: number = nums.reduce((accumulator, currentValue) => accumulator + currentValue)
let leftSum: number = 0 // Initialize leftSum to 0
let rightSum: number = 0 // Initialize rightSum to 0
// iterate through the array
for (let i = 0; i < nums.length; i++) {
// for each index, the sum of elements to the right can be
// derived using the total sum and the left sum
// minus the current element
rightSum = totalSum - leftSum - nums[i]
// Check left sum equals right sum
(rightSum === leftSum) return i // Found the pivot index
// keeping track of the sum of elements
// to the left of the current index
leftSum += nums[i] // Update the left sum for the next iteration
}
return -1 // Return -1 no pivot index is found
}
// choose an array to test
const nums1: number[] = [1, 7, 3, 6, 5, 6] // 3
const nums2: number[] = [1, 2, 3] // -1 none
const nums3: number[] = [2, 1, -1] // 0
console.log('Pivot Point: ', pivotIndex(nums1)) // OUTPUT pivot point 3
A list of other Prefix Sum Problems
2. Two Pointers
The two pointers pattern involves using two pointers (or indices) to simultaneously iterate through a data structure like an array or linked list to find pairs of elements and conditions that meet a specific criteria, checking for palindromes, or merging sorted arrays. The pointers typically move towards each other or through the arrays in a coordinated manner to solve the problem efficiently.
Let's understand the pattern using the LeetCode problem 88. Merge Sorted Array. So we have two arrays nums1 and nums2 sorted in non decreasing order (essentially, this is like regular ascending order, however duplicates are allowed) and two integers m representing the number of elements in nums1, three (excluding the last three empty elements from the right) and n again three, representing the number of elements in nums2 merge the elements of nums2 into nums1.
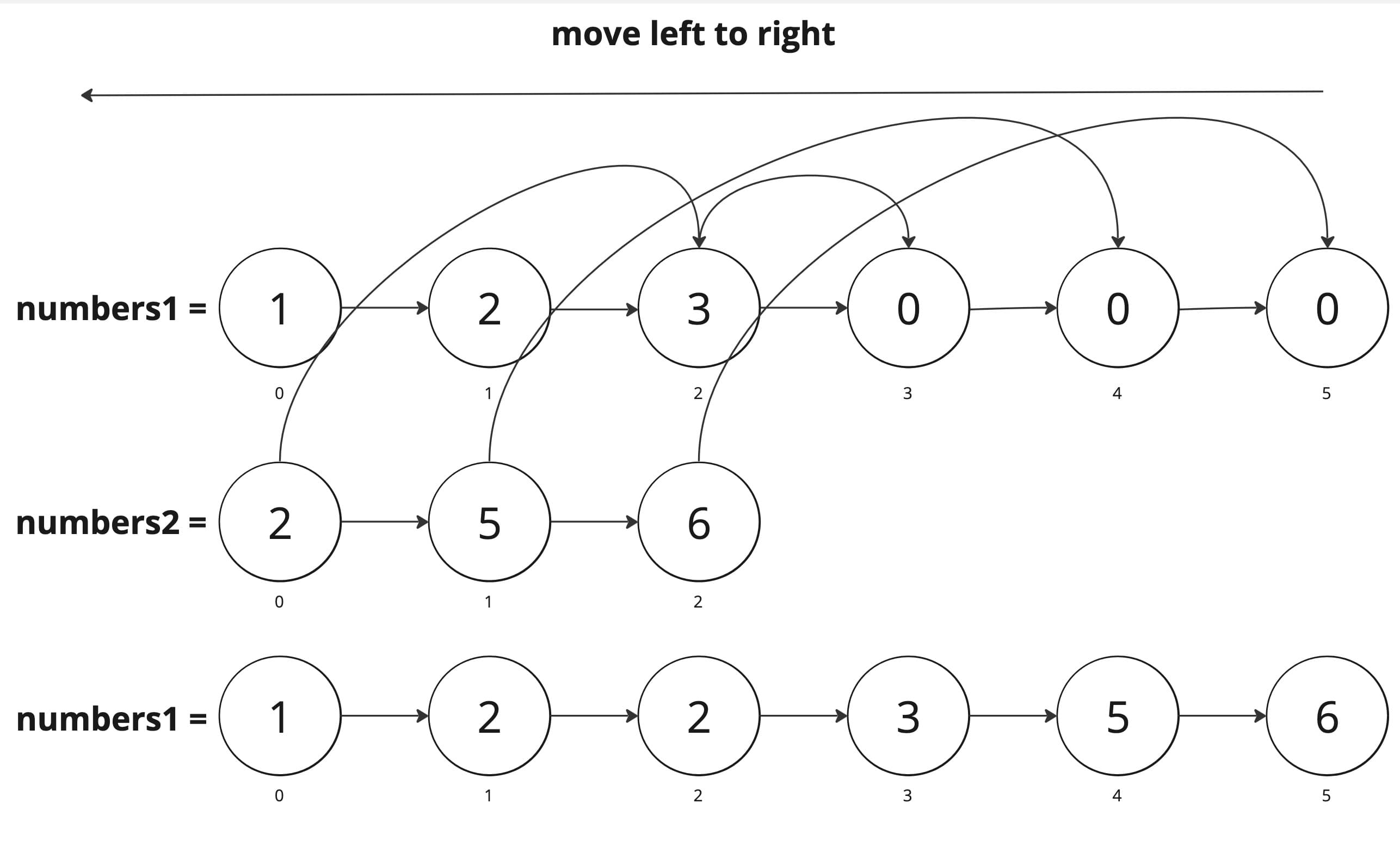
Pseudocode solution for Merge Sorted Array (Brute Force 💪)
function merge(nums1, m, nums2, n):
for i form 0 to n - 1:
nums1[m + i] = nums2[i]
sort(nums1)
const nums1: number[] = [1, 2, 3, 0, 0, 0]
const m: number = 3
const nums2: number[] = [2, 5, 6]
const n: number = 3
merge(nums1, m, nums2, n)
console.log('merged nums2 into nums1 ', nums1)
// OUTPUT: merged nums2 into nums1 Array(6) [ 1, 2, 2, 3, 5, 6 ]
Two Pointers Pattern in TS Solution
Intuition
Since both arrays are already sorted (non-decreasing order), and there is empty space 0 at the end of nums1 array this makes sense to start filling here as it's easier. An end point pointerEnd = m + n - 1 the most efficient way to merge them is to start comparing from the end of both arrays and insert the largest element into the end of nums1. This way, you avoid overwriting elements in nums1 that have not been merged yet as there are duplicates we need to add a check for that.
Step-by-Step Approach:
- Start from the End: Initialize three pointers:
mIndexto track the last element innums1(excluding the extra space)nIndexto track the last element innums2pointerEnd= get the last item innums1(m:3 + n:3 - 1)
- Compare and Place:
- While
nIndexis greater than 0, is not empty.- Validate
mIndexand compare the elements atnums1[mIndex]andnums2[nIndex]. nums1has a size ofm + n, wheremis the number of elements initially innums1andnis the number of elements innums2.- The array
nums1has enough space (sizem + n)0to hold the additional elements fromnums2. - By merging from the back, prevent overwriting any of the elements in
nums1that haven't processed yet. - If
nums2is empty,nums1is already sorted, so no action is needed. - If
nums1is empty, the remainingnums2elements are directly copied tonums1. - This merges the elements from
nums2intonums1in such a way thatnums1remains sorted.
- Validate
Complexity
Time complexity: O(𝑛) - The algorithm involves a single pass through the elements of the array, so the time complexity is linear with respect to the number of elements, 𝑛.
Space complexity: O(1) - The algorithm uses a constant amount of extra space, regardless of the input size, as it mainly operates in-place.
This approach ensures that the merge is done in O(m + 𝑛) time and uses O(1) additional space.
function merge(nums1: number[], m: number, nums2: number[], n: number): void {
// Start from the End: Using three pointers:
/** to track the last element in `nums1`
(excluding the extra space) */
let mIndex = m - 1
// to track the last element in `nums2`
let nIndex = n - 1
/** get the last item in `nums1`
(`m:3 + n:3 = length - 1`) */
let pointerEnd = m + n - 1
/** Merge nums1 and nums2 starting from the end
While there are elements in nums2 to merge */
while (nIndex >= 0) {
/** Compare elements from nums1 and nums2
and place the larger one at the end */
(mIndex >= 0 && nums1[mIndex] > nums2[nIndex]) {
nums1[pointerEnd] = nums1[mIndex] // Place element from nums1 at end
mIndex-- // Move the pointer in nums1 to the left
} else {
nums1[pointerEnd] = nums2[nIndex] // Place element from nums2 at end
nIndex-- // Move the pointer in nums2 to the left
}
pointerEnd-- // Move the end pointer to the left
}
}
// test solution
const nums1: number[] = [1, 2, 3, 0, 0, 0]
const m: number = 3
const nums2: number[] = [2, 5, 6]
const n: number = 3
merge(nums1, m, nums2, n)
console.log('merged nums2 into nums1: ', nums1)
// OUTPUT merged nums1: Array(6) [ 1, 2, 2, 3, 5, 6 ]
A list of Two Pointers problems
3. Sliding Window
The Sliding Window pattern is an efficient approach for dealing with problems involving contiguous sub arrays or substrings. It leverages the fact that you can update the properties of a window incrementally as it "slides" across the array or string, avoiding the need for redundant calculations and significantly improving performance in many cases.
- Fixed-Length Sub arrays: Problems where you need to compute something over all subarrays of a fixed length
- Variable-Length Sub arrays: Problems where you need to find the smallest or largest subarray that meets a certain condition.
- Optimization Problems: Problems where you're optimizing a condition over a subarray (e.g., finding the maximum sum, longest subarray with at most
kdistinct elements, etc.).
Let's understand the pattern using the LeetCode problem 643. Maximum Average Subarray I Find the maximum average of a contiguous subarray length equal to k in a given array of integers.
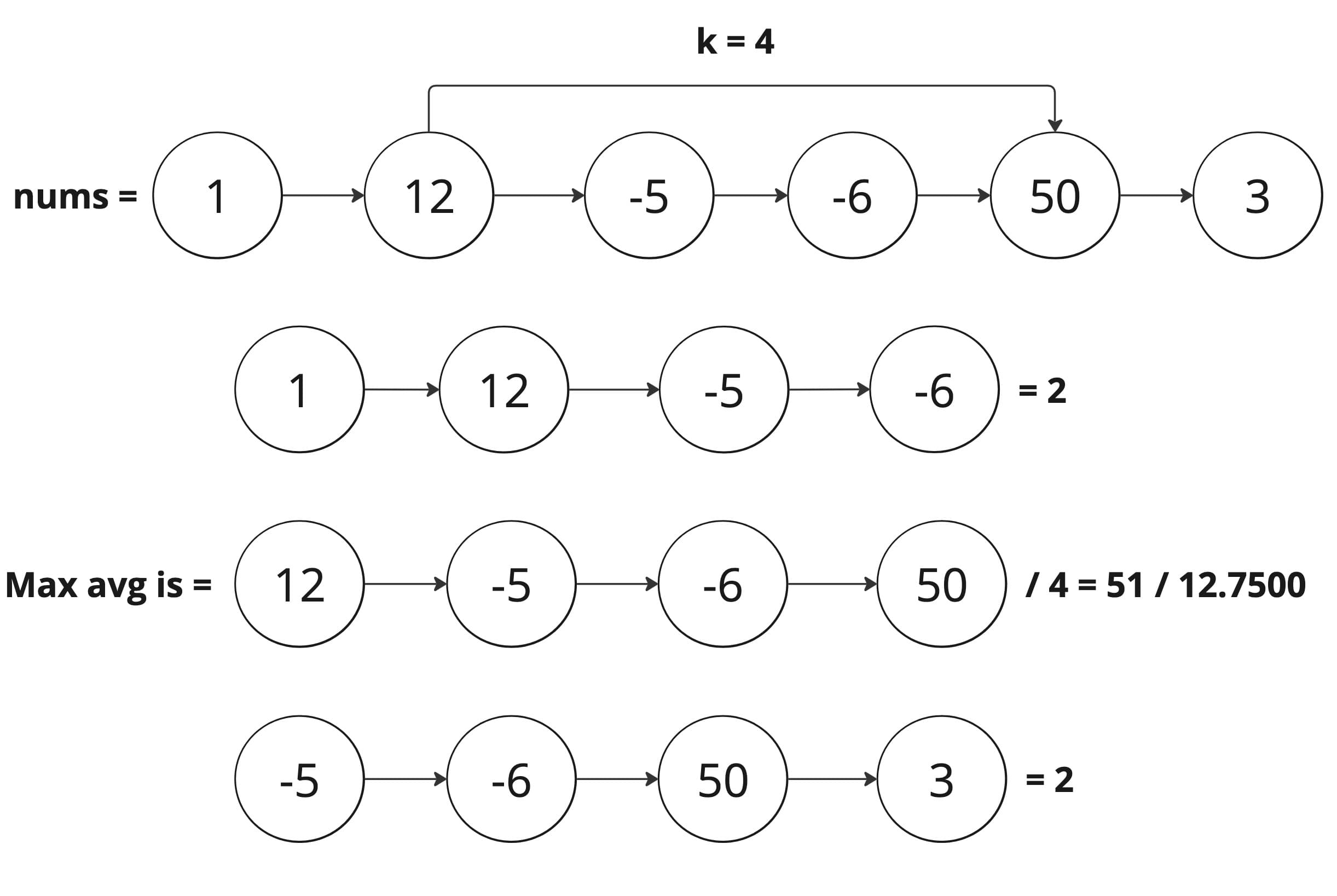
Pseudocode solution for Maximum Average Subarray I (Brute Force 💪)
function findMaxAvgBruteForce(nums, k):
// initialize maxSum to the smallest possible value
maxSum = -Infinity
// Outer loop to iterate through each starting index of subarrays of length k ensuring all subarrrays are considered
for i from 0 to nums.length - k:
// initialize a currentSum to compare with maxSum
currentSum = 0
// Calculate the sum of the subarray of length k starting at index i
for j from i to i + k - 1:
currentSum += nums[j]
// Update maxSum if currentSum is
if currentSum > maxSum:
maxSum = currentSum
// Calculate and return the maximum
return maxSum / k
const nums[] = [1, 12, -5, -6, 50, 3]
const k: number = 4
console.log(findMaxAvgBruteForce(nums, k)) // 12.75
Sliding Window in TS Solution
Intuition
The sliding window pattern is the most efficient solution to this problem. Using it to manage and update the sum of the subarray of length k dynamically avoiding the need to repeatedly get the maxSum, like in the brute force solution.
Step-by-Step Approach:
- Initialize
currentSum:
- calculate to the sum of the first
kelements, to set up the initial window. - use a for loop to calculate the sum of the first
kelements of the array.
- Sliding Window:
- initialize
maxSumand assign tocurrentSum - slide the window one element at a time across the array from start to end of the array.
- update the window
currentSumfor each iteration by subtracting the element that leaves the window from the leftnums[i - k]and add the new element from the rightnums[i]This step avoids recalculating the sum ofkelements every time, by performing only two operations: subtraction and addition
Update maxSum: by comparing
maxSumand the updatedcurrentSumusingMath.maxreturning the largest of the numbers given as input parameters, or -Infinity if there are no parameters.Calculate Average:
return maxSum / kto get the maximum average.
Complexity
Time Complexity: O(𝑛). Iterate through the array once, updating the sum of the subarray in constant time.
Space Complexity: O(1). It also uses a constant amount of extra space regardless of the input size.
const findMaxAverage = (nums: number[], k: number): number => {
let currentSum: number = 0
// sum of the first k elements is calculated using a for loop initialize window
for (let i = 0; i < k; i++) {
currentSum += nums[i]
}
// Initialize maxSum with the sum of the first window
let maxSum: number = currentSum
// Slide the window from start to end of the array
for (let i = k; i < nums.length; i++) {
// Update the window sum by subtracting the element that goes out and adding the new element
currentSum = currentSum - nums[i - k] + nums[i]
// Update the maximum sum found so far
if (currentSum > maxSum) {
maxSum = currentSum;
}
}
// Calculate and return the maximum average
return maxSum / k
}
const nums: number[] = [1, 12, -5, -6, 50, 3]
const k: number = 4
console.log(findMaxAverage(nums, k)) // 12.75 or 12.750000
A list of Sliding Window Problems
4. Fast & Slow Pointers
Also called "Floyd’s Tortoise and Hare algorithm"
Let's understand the pattern using the LeetCode problem 141. Linked List Cycle is there a cycle with in the linked list a cycle being a node that does not point to null or the next node and creates a cycle of infinite loop.
A cycle occurs when a node's next pointer points to a previous node, creating a loop that does not end at null. Determine if a linked list has a cycle, identify a way to detect this loop efficiently. One straightforward (brute force) method would be to traverse the list and keep track of all visited nodes. If we revisit a node, we know there is a cycle. However, this requires additional space to store a Set of the visited nodes.
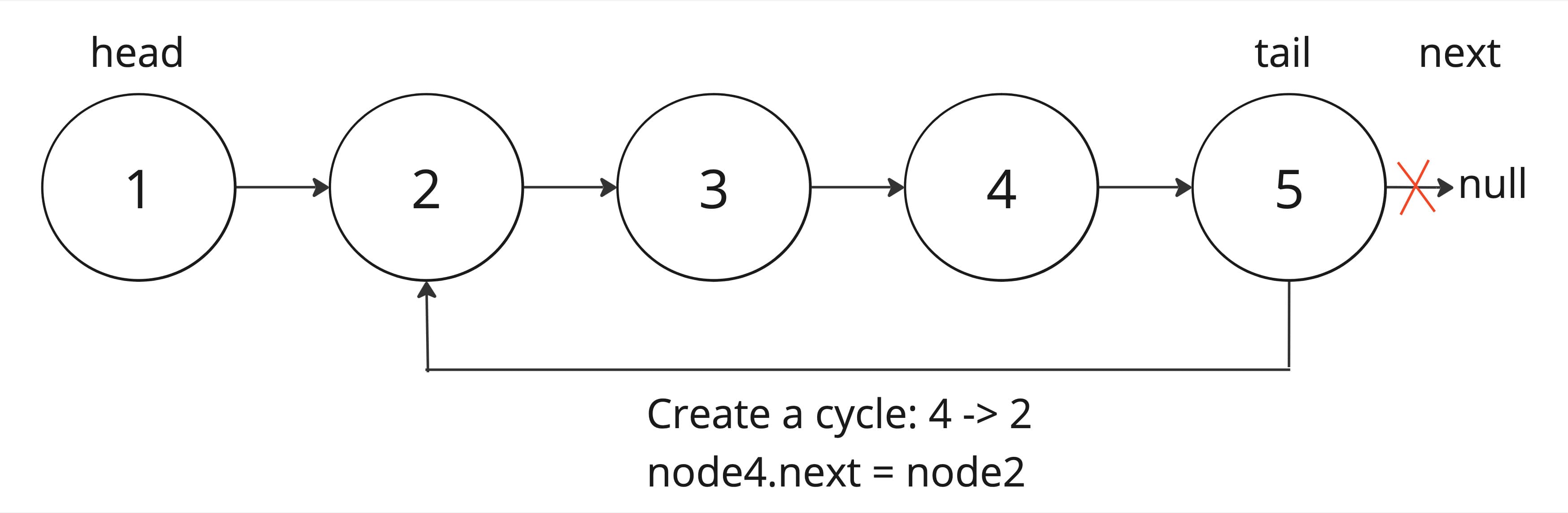
Pseudocode solution for Linked List Cycle (Brute Force 💪)
function hasCycleBruteForce(head):
if head is null or head.next is null:
return false // Empty list or single node, no cycle
// Create a set to store the visited nodes
visitedNodes = new Set()
// Initialize currentNode to the head of the list
currentNode = head
// Loop through the linked list
while currentNode is not null and currentNode.next is not null:
// check if the current node is in the set
if visitedNodes has currentNode:
return true // Cycle detected
// Insert a new element current node to the set
add currentNode to visitedNodes
// Move to the next node
currentNode = currentNode.next
return false // no cycle detected
// Create nodes to test for cycle
const node1 = new ListNode(1)
const node2 = new ListNode(2)
const node3 = new ListNode(3)
const node4 = new ListNode(4)
// Link nodes: 1 -> 2 -> 3 -> 4
node1.next = node2
node2.next = node3
node3.next = node4
// Create a cycle: 4 -> 2
// node4.next = node2
// No cycle
node4.next = null
console.log('Has Cycle: ', hasCycleBruteForce(node1)) // OUTPUT false
console.log('Has Cycle: ', hasCycleBruteForce(node1)) // OUTPUT true
Fast & Slow Pointers in TS Solution
Intuition
Use two pointers that traverse the list at different speeds: slow (Tortoise) and fast (Hare). The slow pointer moves one step at a time, while the fast pointer moves two steps at a time. If there’s a cycle, the fast pointer will eventually catch up to the slow pointer within the cycle. If there's no cycle, the fast pointer will reach the end of the list (null).
Step-by-Step Approach:
- Check: if
headorhead.nextisnullthere is no cyclereturn false - Initialize two pointers with the
headof the list:
slowPointermoves one step at a timefastPointermoves two steps at a time
- While both
fastPointerandfastPointer.nextare notnull(to ensure safe access tofastPointer.next.next):
- move
slowPointerby one step - move
fastPointerby two steps - if
slowPointerequalsfastPointer,return true(cycle detected)
- Cycle Detection: If the loop exits without the pointers meeting,
return false(no cycle found)
Complexity
- Time complexity: O(𝑛)
- Space complexity: O(1)
/**
* Definition for singly-linked list.
**/
class ListNode {
val: number
next: ListNode | null
constructor(val?: number, next?: ListNode | null) {
this.val = val === undefined ? 0 : val
this.next = next === undefined ? null : next
}
}
const hasCycle = (head: ListNode | null): boolean => {
if (head === null || head.next === null) return false
let slowPointer: ListNode | null = head
let fastPointer: ListNode | null = head
// ensure both the fastPointer and its next element exist before attempting to access fastPointer.next.next
while (fastPointer !== null && fastPointer.next !== null) {
slowPointer = slowPointer.next
fastPointer = fastPointer.next.next
if (slowPointer === fastPointer) return true
}
return false
}
// Create nodes to test for cycle
const node1 = new ListNode(1)
const node2 = new ListNode(2)
const node3 = new ListNode(3)
const node4 = new ListNode(4)
// Link nodes: 1 -> 2 -> 3 -> 4
node1.next = node2
node2.next = node3
node3.next = node4
// Create a cycle: 4 -> 2
node4.next = node2
console.log(hasCycle(node1)) // OUTPUT true
5. In-place Reversal of a Linked List
In-place reversal of a linked list is a common pattern where you reverse the order of nodes in a linked list without using extra space. This is useful for various applications, such as reversing a list of items or undoing operations.
Let's understand the pattern using the Leetcode problem 206. Reverse Linked List When reversing a linked list in-place, you alter the next pointers of the nodes so that they point to the previous node instead of the next one. This requires only a few pointers and does not need extra memory proportional to the list size.
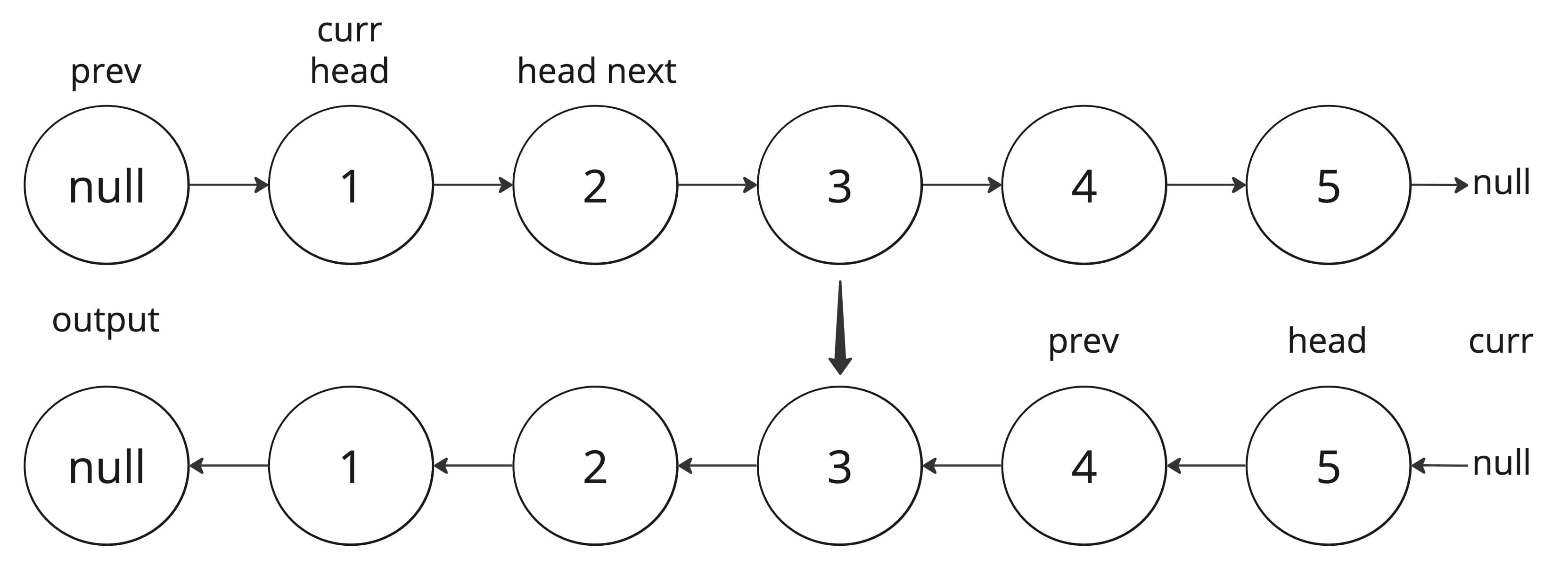
Pseudocode solution for Reverse a Linked List (Brute Force 💪)
function reverseListBruteForce(head):
// Check for empty or single node list
if head is null or head.next is null:
// If yes, return head as there is nothing to reverse
return head
// Initialize an empty array to store nodes
nodes = []
currentNode = head
// Traverse the list and store each node in the array
while currentNode is not null:
add currentNode to nodes
currentNode = currentNode.next
// Reverse the list by updating next pointers
for i from length of nodes - 1 to 1:
// Set the next pointer of the current node to the previous node
nodes[i].next = nodes[i - 1]
// Handle the new tail
nodes[0].next = null
// Return the new head
return nodes[length of nodes - 1]
LinkedList In-place Reversal in TS Solution
Intuition
Reversing the list is about flipping the direction of the pointers, by creating two pointers to keep track of current and previous nodes retracing the path backwards transforming the list step by step
Step-by-Step Approach:
- Initialize pointers:
prevtonull.currtohead.
- Iterate Through the List:
- While
currhas no value or is notnull, until you reach the end. - Initialize
nextwithcurr.nextto store thenextvalue. - Reverse the current node's pointer by setting curr.next to
prev. - Move pointers one step forward set
prevtocurrandcurrtonext.
- While
- Return the new head
prevnow points to the head of the new reversed list
Complexity
- Time Complexity: O(𝑛)
- Space Complexity: O(1)
/**
* Definition for singly-linked list.
**/
class ListNode {
val: number
next: ListNode | null
constructor(val?: number, next?: ListNode | null) {
this.val = val === undefined ? 0 : val
this.next = next === undefined ? null : next
}
}
const reverseList = (head: ListNode | null): ListNode | null => {
let prev: ListNode | null = null
let curr: ListNode | null = head
while (curr !== null) {
const next: ListNode | null = curr.next // get the next node
curr.next = prev // set the next to the previous node reverse
prev = curr // move the node previous to current
curr = next // move to the next node in line
}
return prev
}
// Create nodes to test
const node1 = new ListNode(1)
const node2 = new ListNode(2)
const node3 = new ListNode(3)
const node4 = new ListNode(4)
const node5 = new ListNode(5)
// Link nodes: 1 -> 2 -> 3 -> 4
node1.next = node2
node2.next = node3
node3.next = node4
node4.next = node5
console.log(reverseList(node1)) // 5, 4, 3, 2, 1
6. Breadth-First Search (BFS)
Breadth-First Search (BFS) is a method for exploring or searching through a tree or graph. Imagine you are in a room with several doors, and you want to explore all rooms connected to the current one before moving deeper into any one branch or like reading lines in a book from the top to the bottom. BFS explores all neighbors (or adjacent nodes) at the present depth level before moving on to nodes at the next depth level.
Let's understand the pattern using the Leetcode problem 102. Binary Tree Level Order Traversal this is the first medium problem, all others so far have been easy. Given the root of the binary tree return the level order if the root is empty return empty array [].
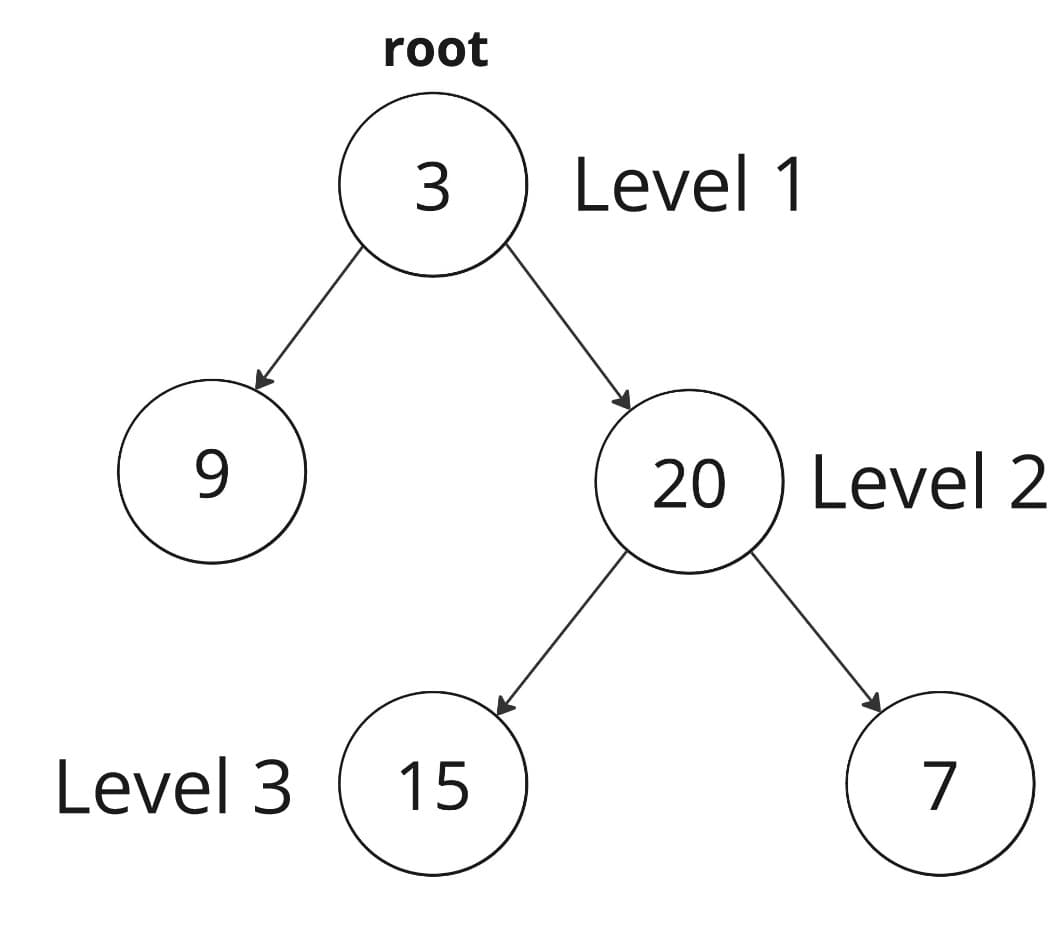
The above linked list output is [[3], [9, 20], [15, 7]]
Pseudocode solution for Binary Tree Level Order Traversal (Brute Force 💪)
function levelOrder(root):
// Check if the root is none (empty tree)
if root is null:
return []
// Initialize result list store the final level
// order traversal
result = []
// Initialize the queue with the root node
queue = [root]
// Traversal of queue until the queue empty
while queue is not empty:
// Get the number of nodes at the current level
levelSize = length of queue
// List to store of nodes at the current level
currentLevel = []
// Process all nodes at the current level
for i from 0 to levelSize - 1
// Remove the first element from the queue
node = queue.shift()
// add the node value to the current level
currentLevel.push(node.val)
// If the left child exists
if node.left is not null:
// add left node for the next level
queue.push(node.left)
// If the right child exists
if node.right is not null:
// add right node
queue.push(node.right)
// Add the current level list to the
// result list
result.push(currentLevel)
// List levels containing the values of nodes in level order
return result
BFS Pattern in TS Solution
Intuition
Level order traversal visits all nodes on one level of the tree before moving to the next level. Using a queue and a head pointer to keep track of the nodes to visit next, visiting nodes one by one.
Step-by-Step Approach:
- Check if the binary tree is empty: if yes return empty array / list.
- Initialize:
- The result list to store the final level order traversal.
- The queue to create and initialize a queue with the root of the tree to store levels.
- The head pointer to simulate a dequeue by maintaining a head pointer.
- Process each level using a while loop:
- Determine the number of nodes at the current level until the head pointer is less than the length of the queue.
- Process level by level:
- At each level, determine the number of nodes (queue size)
- Visit each node, adding it's value to the current level's list and add it's children to the end of the queue for the next level.
- Move to the next level:
- Continue with the next set of nodes in the queue after visiting all nodes at the current level.
- Return the result: list contain the level order traversal.
Complexity
- Time Complexity: 𝑂(𝑛) Each node is visited once. this is the main difference, as the brute is 𝑂(𝑛^2) in worst case.
- Space Complexity: 𝑂(𝑛) The queue can grow to the size of the largest level in the tree, same as the brute force.
/**
* Definition for a binary tree node.
* TreeNode Class: Defines the structure of a node in the binary tree, with a value and pointers to left and right children.
* */
class TreeNode {
val: number
left: TreeNode | null
right: TreeNode | null
constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
this.val = val === undefined ? 0 : val
this.left = left === undefined ? null : left
this.right = right === undefined ? null : right
}
}
const levelOrder = (root: TreeNode | null): number[][] => {
// Initial Check: If the tree is empty, return empty list.
if(root === null) return []
// Initialize result list store the final level
// order traversal
const result: number[][] = []
// Queue Initialization: Start with a queue containing the root node
const queue: TreeNode[] = [root]
// Simulate a dequeue by maintaining a head pointer
let head: number = 0
// Traverse queue until the all
// nodes have been processed
while (head < queue.length) {
// Determine the number of nodes at the current level (levelSize).
const levelSize: number = queue.length - head
// Initialize an array to store the values of nodes at the current level
const currentLevel: number[] = []
// Use a loop to process all nodes at the current level
for (let i = 0; i < levelSize; i++) {
// Dequeue the current node
let node: TreeNode = queue[head++]
/** Add the current node value to the
level list */
currentLevel.push(node.val)
// Enqueue if left node exists
if (node.left !== null) {
queue.push(node.left)
}
// Enqueue if right node exists
if (node.right !== null) {
queue.push(node.right)
}
}
/** Store Current Level:
After processing all nodes at
the current level, add the currentLevel
list to the result */
result.push(currentLevel)
}
/** Return the result list contain
the level order traversal */
return result
}
// Input:
const root = new TreeNode(3)
root.left = new TreeNode(9)
root.right = new TreeNode(20)
root.right.left = new TreeNode(15)
root.right.right = new TreeNode(7)
console.log(levelOrder(root)) // Output: 0: Array [3] 1: Array [9,20] 2: Array [15,7] length: 3
Start Over with NeetCode 150
It was a this point (a pivotal moment in this learning adventure) after revisiting and solidifying the first pattern.Instead of learning a new pattern I decided to write this post LeetCode Starting Over with NeetCode
7. Overlapping Intervals
The Overlapping Intervals pattern is to find all intervals that overlap. An interval is represented as a pair of values like [start, end]. For example tow intervals [a, b] and [c, d] overlap if they share at least one common point.
Let's understand the pattern using the LeetCode problem 56. Merge Intervals Another medium LeetCode problem sort each interval, overlapping intervals should be adjacent, iterate and build solution; also graph method, less efficient, more complicated.
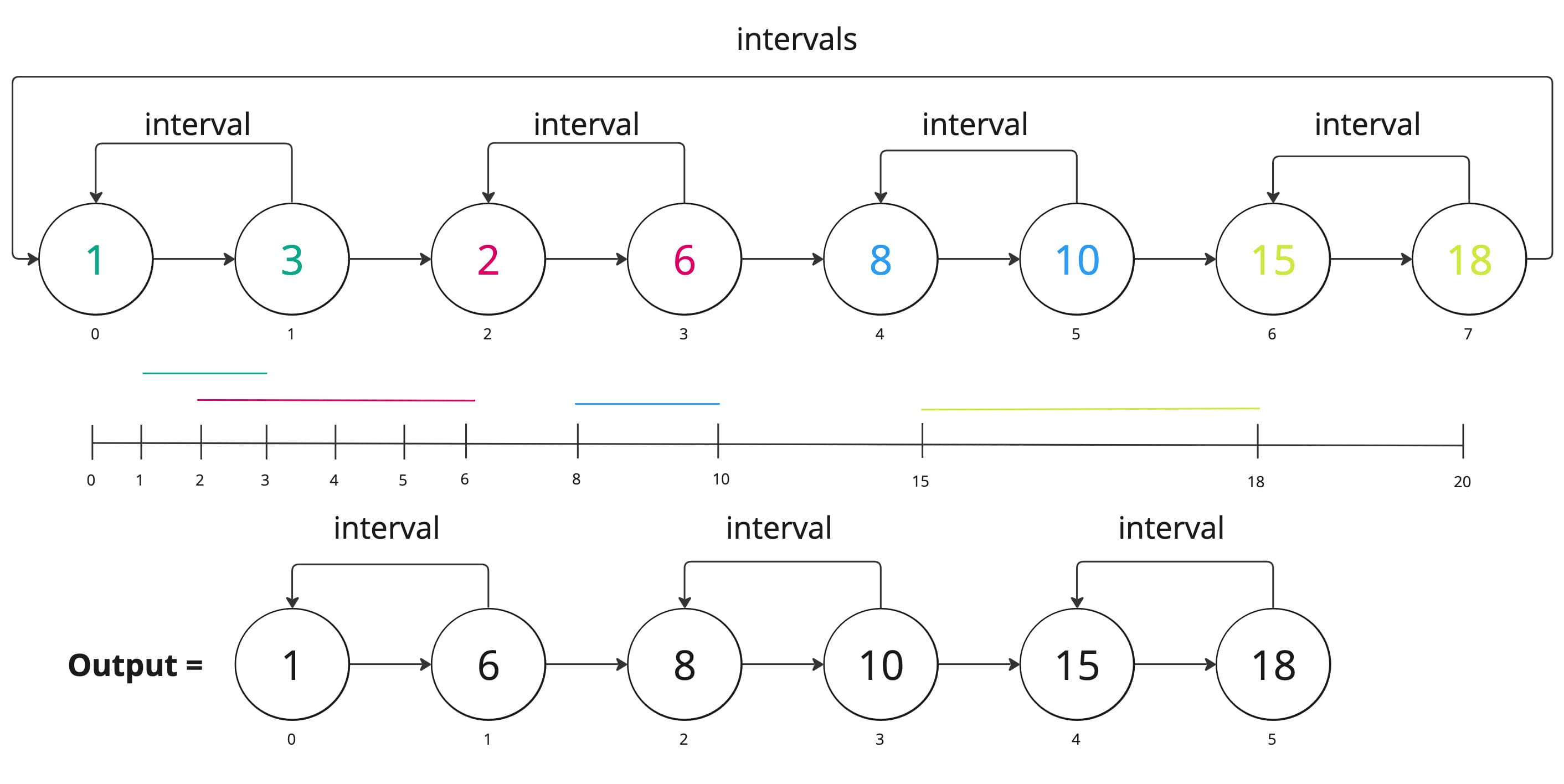
Pseudocode solution for Merge Intervals (Brute Force 💪)
function mergeIntervals(intervals):
// Check if the intervals list is empty
if(intervals.length === 0)
return []
result = []
// Sort intervals based on their start values
while intervals.length > 0:
interval = intervals.pop()
let merged = false
// Loop thru the intervals in the result
for i from 1 to intervals.length - 1:
// Check if the current interval overlaps with the interval in the result
if interval[0] <= result[i][1] && interval[i] >= result[i][0]):
// Merge intevals by updating start and end
result[i][0] = min(result[i][0], interval[0])
result[i][0] = max(result[i][1], interval[1])
merged = true
break
if not merged:
// If no overlap, add the current interval to the result
add interval to result
return result
Overlapping Intervals in TS solution
use sort to
Intuition
Step-by-Step Approach:
Complexity
- Time Complexity: 𝑂(𝑛log𝑛)
- Space Complexity: 𝑂(𝑛)
const merge = (intervals: number[][]): number[][] => {
if (intervals.length === 0) return []
// sort intervals
intervals.sort((a, b) => a[0] - b[0])
const result: number[][] = [intervals[0]]
for (let i = 0; i < intervals.length; i++) {
const current: number[] = intervals[i]
const lastInterVal: number = result[result.length - 1]
if (current[0] <= lastInterVal[1]) {
lastInterVal[1] = Math.max(lastInterVal[1], current[1])
} else {
result.push(current)
}
}
return result
}
const intervals: number[][] = [
[1, 3],
[15, 18],
[8, 10],
[2, 6],
]
console.log('merge if overlap: ', merge(intervals)) // [ 1, 6 ], [ 8, 10 ], [ 15, 18 ]
Merge Intervals - Sorting - LeetCode 56
Outline of These Posts
For 28 Days LeetCode Part 1 and Part 2, I will be following these patterns:
- AlgoMaster LeetCode Patterns: 14 LeetCode problems.
- leetpattern
My helpers / teachers along the way will be:
By leveraging these resources, I aim to systematically and effectively prepare for technical interviews. Each post will document my journey, offering insights into my process, challenges, and solutions, ensuring a thorough and reflective preparation.
Reference
Medium Big O notation time and space complexity
Geeks for Geeks difference between BFS and DFS/
geeks for geeks data-structures
LeetCode study-guide Solved 1000 problems Here are some of my learnings
FreeCodeCamp best-free-courses-to-learn-data-structures-and-algorithms-in-depth
Photo Credits
Photo by Dan Senior on Unsplash